算法
相关题目#
https://blog.csdn.net/SmallTeddy/article/details/108510523
https://juejin.cn/post/7012922543044558862
https://leetcode-cn.com/problems/find-all-duplicates-in-an-array/
堆栈的区别?#
https://zhuanlan.zhihu.com/p/60336501
- 管理方式不同。
- 空间大小不同。
- 生长方向不同(堆,由低到高。栈是由高到低。)
- 分配方式不同。(堆是动态分配的,栈可以是由操作系统分配,比如局部变量的分配。)
- 存放内容不同。(具体存放内容是由程序员来填充的,栈存放一些局部变量,寄存器,参数)
- 参考地址:https://blog.csdn.net/k346k346/article/details/80849966
- 参考地址https://kylenxu.github.io/2019/06/17/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E7%9A%84%E5%A0%86%E3%80%81%E6%A0%88%E5%92%8C%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E7%9A%84%E5%A0%86%E5%86%85%E5%AD%98%E3%80%81%E6%A0%88%E5%86%85%E5%AD%98%E7%9A%84%E5%8C%BA%E5%88%AB/
- 堆
- 其实就是咱们程序编译的时候申请的某个大小的内存空间。 也就是动态内存。
- 可以迅速找到一堆数中最大或最小值的数据结构
栈和队列的区别?#
- 栈
- 也称为堆栈,是一种先进后出,后进先出的数据结构,删除和插入都在栈顶操作的线性表。 其实就是一种使用堆的方法。
- 数组的最后一项相当于就是栈顶,第一项是栈底。
- 特性:
先进后出,后进先出。- 插入使用
push函数, 删除也就是删除栈顶元素使用pop。 - 栈的应用:
- 函数调用栈
- 浏览器前进和后退
- 队列
- 先进先出的数据结构。就像食堂排队一样,先去的就先打饭。
- 数组的第一项是队头,最后一项是队尾。
- 优先队列,其实就是使用 splice 方法插入
- 队列的应用:
- 广度优先遍历搜索(其实就是多层同事向下遍历,双递归)
- 总结:
- 栈和队列都是一种受限的数据结构。
- 栈是先进后出,后进先出。
- 队列好比核酸检测排队,先进先出的原则。
- 栈和队列是相反的,比如数组的末尾是栈的顶端,数组的开头是队列的头部。
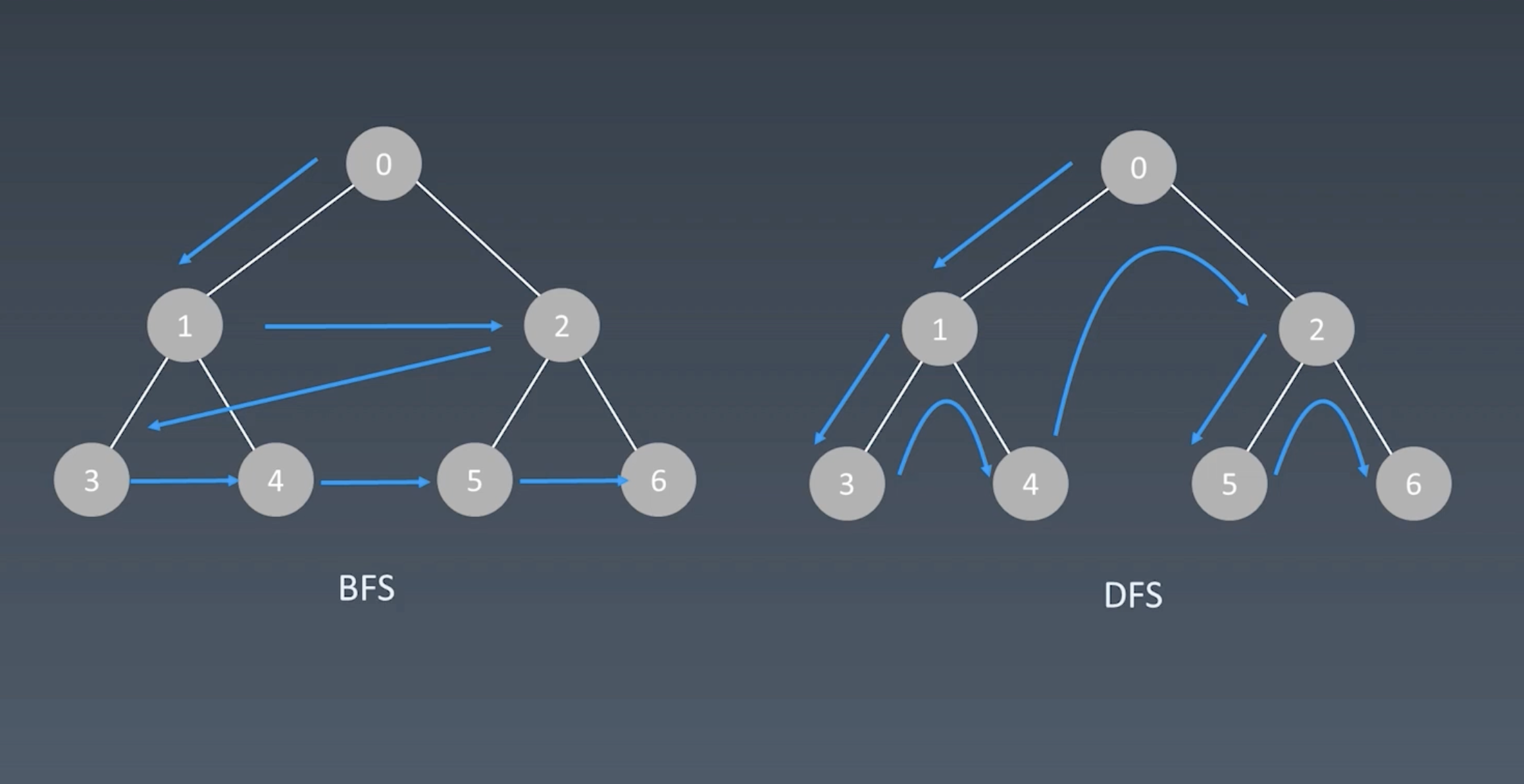
深度优先遍历和广度优先遍历?#
- 深度优先遍历,一次递归向左走到最下面的子节点,然后向右边继续向上回溯。
- 广度优先遍历,就是所有层级节点同事向下进行查找。
- 新建一个队列,从根节点触发。
- 把队头出队
- 把队头的children挨个入队
- 重复2、3步骤,知道队列为空为止
项目用过那些算法?#
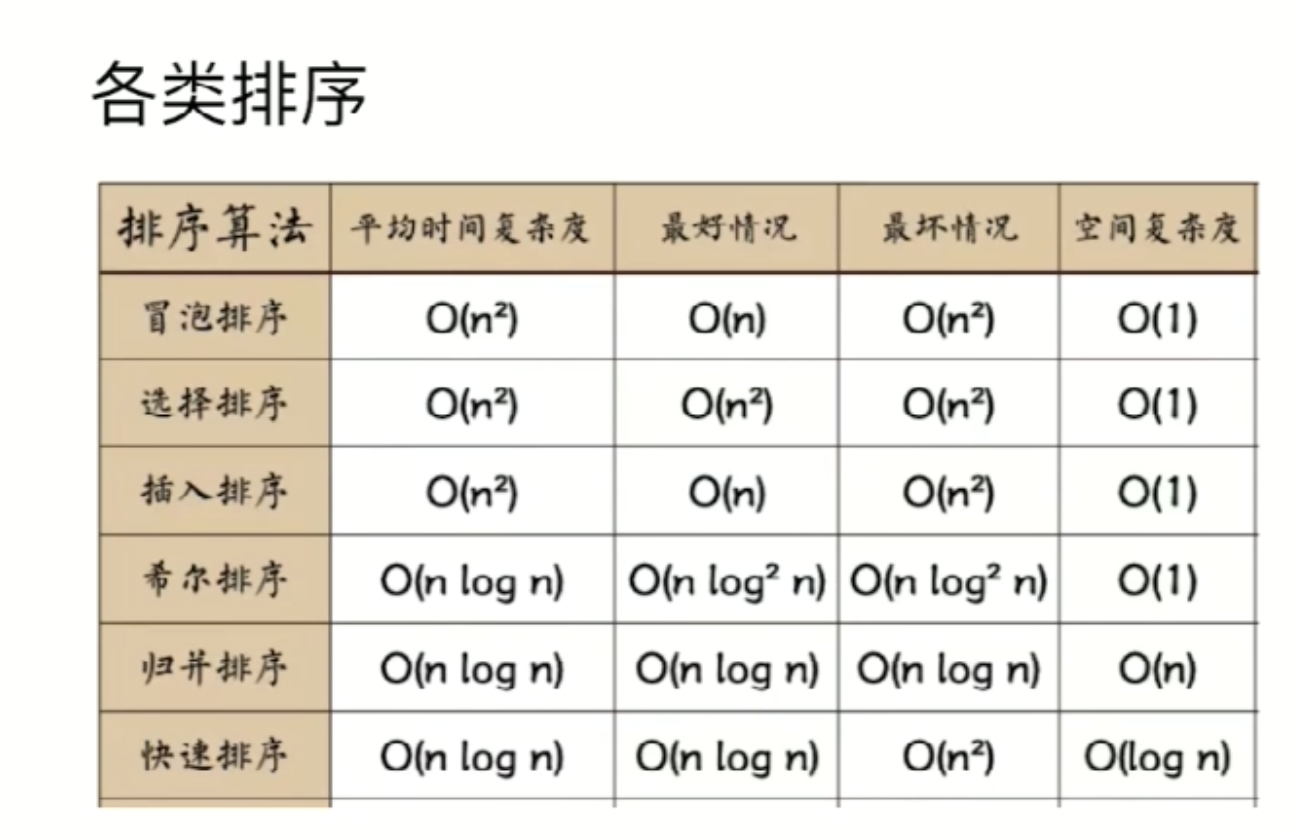
排序算法
了解那些排序算法?#
- 冒泡排序
- 依次遍历数组所有的数,并且递减,如果左边大于右边,那么左右相互交换位置(这里需要定义一个临时变量进行保存当前的值好做替换)。
- 其实就是相邻比较将大的值放到左边
- 因为必须为两个 for 循环,固为 O(n²),空间复杂度也为 O(1)
- 选择排序
- 其实就是选择出一个最小值放到左边。
- 因为必须为两个 for 循环,固为 O(n²),空间复杂度也为 O(1)
- 插入排序
- 其实就是后一个元素与前一个元素相比较,如果后一个元素比前一个元素要小那么插入进去。
- 因为必须为两个 for 循环,固为 O(n²),空间复杂度也为 O(1)
- 归并排序
- 排序分组,最后合并
- 时间复杂度为O(nlogn),空间复杂度为O(n)
- 快速排序
- 时间复杂度为O(nlogn),空间复杂度为 O(logn)
参考地址:http://data.biancheng.net/view/117.html
数组和链表的区别?#
- 数组是基于索引的数据结构,每个元素跟索引相关联。
- 链表依赖于引用,是由一组不必相连【不必相连:可以连续也可以不连续】的内存结构 【节点】,按特定的顺序链接在一起的抽象数据类型。
- 线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer),由于不必须按顺序存储,链表的插入和删除操作可以达到O(1)的复杂度。
- 如果你的代码对内存的使用非常苛刻,那数组就更适合你。因为链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针,所以内存消耗会翻倍。而且,对链表进行频繁的插入、删除操作,还会导致频繁的内存申请和释放,容易造成内存碎片,触发语言本身的垃圾回收操作。
参考地址:https://segmentfault.com/a/1190000019823552
- 数组底层有一个内存管理器的东西。每当你申请数组的话,计算机实际在内存中给开辟了一段连续的地址,每一个地址的话可以通过内存管理器进行访问。访问第一个还有访问第任何一个元素的时间是一样的,所以访问速度快。
- 数组相当于一个柜子,有很多抽屉。假设我们先存储了三个数据,这时候我们需要添加第四个数据的时候,前面的抽屉被占用了,那么需要请求计算机重新分配一块,可以容纳四个数据的内存,然后还需要将数据迁移过去。如果再来一个数据,依次反复进行。
数组的缺点:显而易见就是插入的时候会很慢。- 链表
其实就是有两个成员变量一个是
value,另一个是next指针指向下一个成员,串起来形成链表。- 如果只有一个 next 指针的话,那么就是
单链表,如果有 prev或者previous,那么既可以指向前面,又可以指向后面,称为双向链表。 头指针一般用head表示,尾指针用tail表示,最后一个元素他的next指针为空,也可以指回到head来,可以叫做循环链表。 进行链表的删除增加操作,链表不需要挪动元素,还有复制元素。- 链接存储在内存的任何地方,不要求连续,每个元素存储了下一个元素的地址。就好比看电影选座位,我们同性朋友一起,可以选择不连续的座位,可以隔开。
- 就像一个火车,每一列卸载自己的乘客(item),还要与下一节火车相关联(next)
- 链表学习地址:https://www.bilibili.com/video/BV1SJ41117ui?p=9&spm_id_from=pageDriver
总结:- 数组插入数据需要连一起,如果内存空间不连续就得全体迁移,甚至出现内存空间足够但是由于不在一起而导致无法为数据分配内存。
- 链表插入数据不需要移动数据,所以速度快,而且避免了内存空间足够但是连续空间不足导致无法分配内存的情况。
数组优点:由于数组在内存中连续,我们可以轻松知道每个元素的内存地址。用数组的起始位置 + 数组大小 * 元素编号,那么随机访问的速度就很快了,而链表因为不连续无法计算出每个元素的内存地址就需要一个个往后去找了,因此访问速度慢。其实就是数组插入慢,需要分配内存,不连续就全部得迁移。链表的话,不需要移动数据,所以插入数据快。数组的话是连续的,访问速度快,链表不连续,需要一个个的去查找,所以访问速度慢。
快排是一种什么思想?#
- 递归分治的思想
快排时间复杂度是多少?#
- O(nlogn)
快排适用于哪些场景?#
- 其实就是用于乱序的数组
树形结构怎么查找某一个节点?(二叉查找树)#
- 先遍历左子树,再遍历右子树。
- 比父节点小的放左边,大的放右边,依次延伸----就和快速排序差不多,小的放左边,大的放右边。
- 二叉树也可以进行排序,非线性结构,有利于删除和插入。
特点:
- 每一个节点上最多只有两个节点
- 每个节点的左子节点都是小于自己的
- 每个节点的右子节点都是大于自己的
- 总结就是:每个节点左边都是依次减小的,每个节点的右边都是依次增大的。
参考视频:
- https://www.bilibili.com/video/BV1L34y127rT?from=search&seid=10906841747140060601&spm_id_from=333.337.0.0
- https://www.bilibili.com/video/BV1d54y1q7k7/?spm_id_from=autoNext
链表中的跳表?#
只能用于链表有序的情况- 其实就是直接找
next的next,跳过中间一个。这只是跳一级,跳更高的话,那么就是直接第一项的next指向中间的当前项。
如果是删除操作是选择数组还是链表呢?#
- 删除选链表,因为不需要移动数据。
二叉树删除#
- 第一种情况:删除的节点下面有左子树或者右子树,那么直接继承上一个父节点就可以了。
- 第二种情况:删除的节点下面有左子树并且也有右子树的话,
- 第三种情况:删除的节点下面有多个节点?
- 如果你想相对于删除的这个节点小一点的话,也就是去左子树找最大值
- 如果你想相对于删除的这个节点大一点的话,也就是去删除节点的右子节点的左子树找最小值。
- 参考地址:https://www.bilibili.com/video/BV174411P7bc?p=23&spm_id_from=pageDriver
- 总结:
- 如果左右节点没有值说明是叶子节点删除就行。
- 如果左右节点有一个值,父节点等于删除节点的左节点或者右节点即可。
- 如果删除的节点有多个节点,那么考虑得就比较多了,有两种方式,只说一种就行,就是往删除节点的右子树找比右子树找最小的节点就可以了。
递归和迭代的区别?#
- 递归:常用算法,构造嵌套的树形结构的时候。分治算法,递归效率不搞,
- 迭代,就是将上一次计算的结果传递参数到下一次。会优先考虑迭代
- 其实就是,不断回到同一个场景并优化解决与不断下潜至底层并解决的区别。
- 递归是自己调用自己,每次旨在缩小问题规模。迭代是自己执行很多次,每次旨在更接近目标。
总结:- 他们的共同点在于,描述一个多次操作。
- 不同点在于:
- 【循环】描述每次的操作和上一次操作相同之处。
- 【迭代】描述每次的操作和上一次操作不同之处
快排如果有重复的数据是怎么优化的呢?#
- 其实如何比他小的放到右边数组中
- 如何重复或者比它小的直接放到右边。下次递归继续
时间复杂度和空间复杂度#
排序算法#